Exec Summary
- Quantum computing uses the principles of quantum mechanics to implement new means of processing information
- Quantum computing uses qubits, which can represent two states simultaneously
- Quantum cryptography uses the principles of quantum mechanics to implement algorithms that are secure against both quantum and classical cryptography
- Quantum cryptanalysis using the principles of quantum mechanics to effectively attack classical cipher systems
- The quantum algorithms Shor's algorithm and Grover’s algorithm enable quantum attacks on classical cryptosystems.
- Shor’s algorithm allows for much more efficient factoring of large numbers and computing of discrete logarithms — the hard problems behind RSA, DSA, Diffie-Hellman, and Elliptic Curve Cryptography
- Grover’s algorithm speeds up brute-force searches, cutting the effective security of symmetric algorithms like AES in half
- Post quantum cryptography (PQC), alternatively called “quantum resistant cryptography” protects against these attacks.
What is Quantum Computing?
Quantum computing is a rapidly advancing field that leverages the principles of quantum mechanics to perform calculations, specifically using superposition, entanglement, and quantum interference. These allow certain calculations which are very difficult for classical computers to perform to be done much more efficiently, which has relevance to the security of cryptographic systems.
Key Principles of Quantum Computing
While classical computing allows operations on collections of bits, each representing a one or a zero, quantum computing uses 'qubits' (quantum bits), which can operate on more than one state at a time by using quantum superposition. 2 qubits can operate on 2^2 units of information, 3 qubits on 2^3 units of information and so forth. By comparison, 3 classical bits can represent only one specific value in the range of 0-7.
Further, qubits can be entangled in such a way that the state of one qubit is connected to the state of another, which allows for certain highly efficient computations in quantum systems, as well as secure communication over long distances.
Quantum interference can be used to manipulate probabilities, amplifying correct solutions and cancelling out incorrect solutions in certain problems.
In combination these principles theoretically allow quantum computers to solve problems that are intractable for classical computers, including many algorithms used in asymmetric (public key) cryptography systems such as RSA and ECC.
Cryptographic Cover Time
Cryptographic cover time is an important concept to have in mind when looking into quantum computing and its impact in the cryptanalysis of current algorithms.
Put simply, cryptographic cover time is the time that a cryptosystem will protect the data it has encrypted, before advances in computing power or other technologies render the cryptosystem weaker or even break it entirely.
For some data, perhaps that contained within a TLS connection for a read-only browsing scenario, the time needed for cover might be relatively short. For others, perhaps sensitive national security relevant data, the time needed for cover might be in terms of decades or centuries.
The development of quantum computing, as mentioned above, will change the cover time achievable dramatically for some algorithms, and further, if one’s threat model includes adversaries with the capabilities to record and store network data, it is quite possible that once quantum computing advances to the point of being able to break RSA-2048 or ECC ciphers, the entire conversation recorded can be broken and the cleartext revealed.
Given this, while the current recommendation by NIST is to move to quantum resistant ciphers by 2030, it may, depending on the threat model, already be too late – if you have sensitive data that has been recorded and stored by your adversary, which will still be valuable in 5 years, this data will be exposed when quantum computing eventually becomes able to break the non-quantum resistant ciphers used.
The State of Quantum Computing
Current Quantum Computing Capabilities
Quantum computing has been theoretically described since the early 1980s and was first practically demonstrated with 2 qubits in 1998. In the time since, many advances in the field have yielded increasingly capable quantum computers, with hundreds of qubits in general purpose designs, and thousands in specialty applications.
Quantum Cryptography Versus Quantum Cryptanalysis
It is very important to make a distinction between quantum cryptography, which is the use of quantum computers to implement cryptographic primitives such as key exchange, signing of data, and non-repudiation, and quantum cryptanalysis, which is the use of quantum computer to break classical cryptosystems. The following sections describe each of these, starting with quantum cryptography.
What is Quantum Cryptography?
Because the behavior of quantum computation is rooted in the principles of quantum mechanics, these properties can be leveraged directly to construct provably secure systems of communication, meaning these systems cannot be broken by either classical or quantum computers, assuming a perfect implementation and a lack of any (perhaps not currently known) side-channels or other flaws. We’ll take as example quantum key distribution (QKD).
What is Quantum Key Distribution (QKD)?
Quantum Key Distribution is a means to share cryptographic keys between two parties. As is tradition, we will refer to these parties as Alice and Bob and demonstrate this idea by reviewing the BB84 protocol, first developed in 1984, and currently the most widely used form of quantum key distribution.
First, Alice and Bob ensure they have two communications channels, one for the quantum communication (typically a fiber optic connection) and another a classical communication channel (which could be as basic as a phone call or an email).
Next, Alice creates a random binary string and encodes this onto quantum particles, typically photons. These are polarized along different bases (or directions) that represent the 0 or 1 state of the transmitted bits. For example, a horizontal polarization may represent a 0, and a vertical polarization a 1. Additional complexity may be added by adding two diagonal bases to the horizontal and the vertical.
Alice then sends these photons, one at a time, to Bob using the quantum communication channel.
Bob randomly chooses bases to measure the incoming photons. He can only measure one basis at a time, and it won’t always be correct, which leads to the next step, reconciliation.
After the transmission is complete, Alice and Bob compare the bases they used over a classical communication channel. Note that this doesn’t means they share the actual random string sent, just the bases they used when transmitting (Alice) and receiving and measuring (Bob).
For any photon where Alice and Bob used the same base, the results align, and these aligned measurements form a shared cryptographic key.
If Eve, an eavesdropper with access to the quantum channel, attempts to measure the photons, their observation will change the quantum state of the photons, which will introduce discrepancies in the results that Alice and Bob can discern in their reconciliation process. If too many such errors are detected, Alice and Bob can discard the key they are creating and try again.
Finally, once a secure key of the proper length is established Alice and Bob can then use this key in a symmetric algorithm to encrypt communication between them.
What is Post-Quantum Cryptography (PQC)?
Post-Quantum Cryptography refers to cryptosystems which are resistant to attack from both classical and quantum computers. They are specifically designed to address the vulnerabilities of traditional cryptography to quantum attacks, to ensure long-term security for communications and data storage as quantum computers become more capable in the future. Note that these cryptosystems do not have to use quantum properties themselves, only that they must be resistant to attack from both classical and quantum computers.
Currently for key exchange, lattice-based cryptography is the most promising form of post-Quantum cryptography available.
What Traditional Cryptographic Algorithms are Vulnerable to Quantum-Based Attacks?
Broadly speaking traditional cryptographic algorithms can be divided into symmetric algorithms such as AES, and asymmetric/public-key algorithms such as RSA and ECC. Asymmetric algorithms are used primarily in key exchange scenarios, where they allow to parties to arrive on a shared key which is then used in a symmetric system, as well authentication and digital signatures.
Asymmetric cryptographic systems generally rely on "one-way" mathematical problems—operations that are easy to compute in one direction but practically impossible to reverse without the secret key.
RSA depends on the difficulty of factoring very large numbers, and Elliptic Curve Cryptography (ECC) relies on the difficulty of solving discrete logarithms on elliptic curves.
A quantum algorithm known as Shor's Algorithm is highly efficient at solving the mathematical problems underlying many current forms of asymmetric encryption. Using this algorithm a quantum computer can factor large numbers exponentially faster than a classical computer. Likewise, it can efficiently solve discrete logarithm problems.
Unlike symmetric ciphers, extending the key size does not significantly affect the time that Shor’s Algorithm needs to break these systems.
Why Do We Not “Need” PQC for Symmetric Cryptographic Algorithms?
Shor’s Algorithm does not provide any improvements against symmetric encryption. Another quantum algorithm called “Grover’s Algorithm” can be used to search through possible key combinations more efficiently than classical computers can, providing a quadratic speedup. With a classical computer, an exhaustive brute force search requires 2keylength operations, and with Grover’s algorithm, this is reduced to 2keylenth/2.
However, this is easily addressed by simply increasing the key length. While AES 128 would become vulnerable to a quantum-based attack, having its key length reduced to 64-bits, AES-256 is considered to be secure, with a key length of 128 bits, enough to make a brute force search infeasible even by quantum computers.
Hybrid Ciphers in Classical TLS Cryptography
Hybrid ciphers are a cornerstone of secure communication protocols like TLS (Transport Layer Security). They combine the strengths of symmetric and asymmetric cryptography to address the key exchange problem, ensuring both scalability and security in data transmission. Before the advent of public-key cryptography, the only choice was to use symmetric ciphers, requiring all parties to share a pre-distributed secret key. This reliance on shared secrets made key distribution both challenging and risky, as it often necessitated secure physical transport via trusted couriers.
Public-key cryptography revolutionized this process by enabling secure communication between two parties without requiring pre-shared keys. It allows both parties to agree on a session key for symmetric encryption by leveraging asymmetric cryptographic algorithms, such as RSA or ECDH. Once the session key is established, symmetric encryption, such as AES, takes over for fast and efficient data transmission. This hybrid system combines the scalability of public-key cryptography with the performance of symmetric cryptography, creating a secure and efficient framework for session management.
Expanding Hybrid Ciphers to Include Post-Quantum Cryptography
Hybrid ciphers are evolving in response to the emergence of quantum computing, which poses a potential threat to classical cryptographic algorithms as we have noted above. This has led to the development and integration of post-quantum hybrid ciphers in TLS to safeguard cryptographic systems against quantum attacks.
Post-quantum hybrid ciphers expand the classical hybrid cipher model by incorporating quantum-resistant algorithms into the key exchange process. In a post-quantum hybrid key exchange, both a classical (non-quantum-resistant) key exchange protocol and a quantum-resistant key exchange protocol are executed simultaneously. This dual approach ensures backward compatibility with existing systems while preparing for a post-quantum future.
When is PQC Used?
In situations where vulnerable public-key algorithms are used, broadly speaking! One specific example is in TLS, where post quantum cryptography algorithms are used for key exchange purposes.
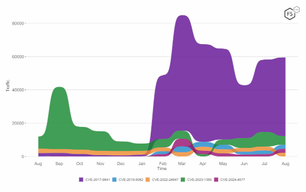
In our survey of the top one million sites (https://www.f5.com/labs/articles/threat-intelligence/the-state-of-pqc-on-the-web), we found that the X25519MLKEM768 was by far the most used hybrid cipher.
X25519MLKEM768 is a post-quantum cryptography key agreement algorithm used in TLS 1.3. It combines the X25519 Elliptic Curve Diffie-Hellman (ECDH) algorithm with the NIST-approved ML-KEM (Modular Lattice-based Key Encapsulation Method) algorithm.
Server and Browser PQC Support
Many web servers support PQC Key exchange, including Apache and Nginx. Several large CDNs also provide it to their customers, including Cloudflare and Fastly.
What Gets Left Behind
Not all clients and servers can be upgraded to use PQC, IoT and non-upgradable devices, legacy OS and browsers, and people that can’t/forget to upgrade will be left behind and left vulnerable.
As ever, with TLS, the problem is rarely with how quickly we adopt new standards, but how quickly we manage to turn off the old (insecure) ones.
Conclusions
It is currently predicted that a quantum computer with only 1 million "noisy qubits" could break RSA-2048 in less than a week. This is a sharp reduction from the previous estimate from 2017 that it would take 20 million such qubits to accomplish this task.
While no such quantum computer currently exists, estimates for the time needed for researchers to build one settle around a decade from now. NIST recommends deprecating vulnerable cryptographic protocols by 2030 and eliminating them entirely by 2035.
It is quite possible that further advancements will either enable the construction of quantum computers with a sufficient number of qubits, or a further reduction in the number of qubits required to perform these attacks, meaning that time is already running out, or perhaps already has.
Recommendations
- As quickly as possible, move towards post-quantum/quantum-resistant technologies everywhere you use cryptography.
- Assess your risk to “harvest now, decrypt later” techniques and take appropriate actions (changing passwords, expiring keys).
- If you are using TLS 1.2 or earlier, immediately move to TLS 1.3. Consider the use of CDNs to provide you with PQC capabilities immediately.
- Think of a future where your most valuable data may be exposed if it is solely protected with classical cryptography and develop plans to protect it with PQC in the next 4-5 years.