Introduction
The NSA’s Information Assurance Directorate1 left many people scratching their heads in the winter of 2015. The directive instructed those that follow its guidelines to postpone moving from RSA cryptography to elliptic curve cryptography (ECC)2 if they hadn’t already done so.
“For those partners and vendors that have not yet made the transition to Suite B elliptic curve algorithms, we recommend not making a significant expenditure to do so at this point but instead to prepare for the upcoming quantum-resistant algorithm transition.”3
The timing of the announcement was curious. Many in the crypto community wondered if there had been a quantum computing breakthrough significant enough to warrant the NSA’s concern. A likely candidate for such a breakthrough came from the University of New South Wales, Australia, where researchers announced that they’d achieved quantum effects in silicon, which would be a massive jump forward for quantum computing.4
Since then, the crypto community has been trying to prepare for the transition to “quantum-resistant” algorithms—that is, algorithms that are secure against an attack by a quantum computer. Let’s look at some of the likely candidates for those algorithms and how they’ll be fitted into the Transport Layer Security (TLS) protocol that we all use today with HTTPS. But first, a bit of explanation.
Quantum Computing Versus Quantum Encryption
Quantum computing, in the context that we’re talking about here, is not to be confused with so-called quantum encryption.
The smallest “bit” of information a normal computer can store is a 0 or 1. A computer with quantum effects can store both values simultaneously in a quantum bit, called a qubit. An array of these qubits can store all possible values simultaneously, but the real significance is that answers to certain problems can be teased out of them at rates that are orders of magnitude faster than an array of conventional bits. A machine with such capability is called a quantum computer. Using conventional, non-quantum computer hardware, it would take 6 quadrillion CPU years5 to factor a 2048-bit RSA decryption key using the number field sieve.6 ;Crypto researchers suggest that it could be done quickly using a single quantum computer with as few as 4,000 qubits.7
When Can I Buy a Quantum Computer from NewEgg?
Up until the NSA missive in 2015, quantum computers were assumed to be decades away. But with the University of New South Wales announcements, and the fact that the NSA itself is spending $80 millionꬷ to develop its own quantum computer, Microsoftꬸ and Google both project that a workable quantum computer capable of decrypting RSA may be achievable by 2025.
Quantum encryption, on the other hand, is a much more specific application of quantum mechanics: it uses the entanglement8 of quantum particles to ensure that a communication has not been eavesdropped on. So, don’t get the two terms mixed up; we’re not talking about quantum encryption. We’re talking about making TLS safe from quantum computing.
If the day ever comes when a real, working, large-scale quantum computer can be built, then the era after that moment will become known as the “post-quantum” era. Encryption algorithms used in the “post-quantum” era should be puzzles that are not easily solved by quantum computers.
What’s the Current Quantum Computing Exposure?
Now that we’ve touched on the theoretical aspects of quantum computing, let’s get down to the nitty gritty and see how quantum computing will affect our current global encryption standard, the Transport Layer Security (TLS), formerly known as SSL. Cryptographers currently believe that only asymmetric encryption algorithms are vulnerable to quantum computing. Unfortunately, these include all the ones we use for TLS protocol handshakes!
- RSA: Vulnerable
- Elliptic Curve Digital Signature Algorithm (ECDSA): Vulnerable
- Elliptic Curve Diffie-Hellman (ECDH): Vulnerable
- Diffie-Hellman (DH): Vulnerable
Interestingly, a 2017 paper, Quantum Resource Estimates for Computing Elliptic Curve Discrete Logarithms,9 by Martin Roetteler, Michael Naehrig, Krysta M. Svore, and Kristin Lauter, appears to confirm suspicions that elliptic curve cryptography (ECC) will fall to quantum computing before RSA does. That may have been another factor in the NSA’s announcement.
Symmetric algorithms (used by bulk encryption) are thought to be safe from quantum computing by merely doubling their key sizes, for example, using AES-256 instead of AES-128.
TLS Refresher—In Case You’re Not an Expert
Quantum computing sounds like it’s going to wreak havoc on TLS, right? Actually, the situation isn’t so bad. Let’s briefly brush up on our basic TLS protocol and see how quantum computing is going to affect it.
The purpose of the TLS protocol is found in its name: transport layer security. TLS is all about securing data in transit. It does this by encrypting blocks of application data called records. The maximum size of an application data record (for TLS 1.2) is approximately 16KB. The TLS record has a pretty simple structure.
| BYTE 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| TYPE | VERSION | LENGTH (214 max.) | APP DATA | ||||
| app data… | |||||||
| app data… | |||||||
| app data… | |||||||
| Checksum [HMAC] | |||||||
The records are encrypted with a so-called symmetric cipher, typically something easy and fast like the Advanced Encryption Standard (AES) or a stream cipher like AES-GCM, which generates a data stream that can be simply XORed with plaintext to create ciphertext.10 The final portion of the record is a hashed message authentication code (HMAC), which is a fancy term for a checksum. The receiver can use the HMAC to determine that the record hasn’t been tampered with or corrupted. The algorithm for the HMAC is typically a variant of SHA with a specific hash key size of 128 or 256 bits. Processing records—encrypting or decrypting them—is actually so easy that you’ll hear it casually referred to as “record processing” or “bulk encryption.”

So, TLS involves two chains of symmetrically encrypted records going back and forth between a client (browser) and a server (web server or application delivery controller). However, before the client and server can start sending these records back and forth in transit, they need to agree on a fast encryption key used to encrypt all the records. They do this by using one of the nifty asymmetric key exchange algorithms mentioned earlier. Because these agreements, called key exchanges, use asymmetric algorithms such as RSA, ECDSA, ECDH, or DH, they are vastly more computationally expensive than the actual record processing itself.
At a high level, then, TLS is just this easy:
Agree on a session key by using an asymmetric key exchange in a TLS handshake
Loop
Symmetrically encrypt and then hash 16KB of data into a record
Transport the record
Decrypt and verify the record
Cake!
How Post-Quantum Computing Will Affect TLS
So, what’s the problem that quantum computing introduces?
Before we look at that, let’s start with the good news, which is that record processing in a quantum computing world will be exactly the same. That’s because the symmetric encryption ciphers (like AES) and HMAC hashing algorithms (like SHA) are thought to be mostly resistant to quantum computing, requiring only a doubling of key size to be resistant until the end of time. According to the NSA’s Information Assurance Directorate, “The AES-256 and SHA-384 algorithms are symmetric, and believed to be safe from attack by a large quantum computer.”11
F5 Labs’ own research (/content/f5-labs/en/labs/articles/threat-intelligence/the-2016-tls-telemetry-report-24674.html) shows that 75% of TLS hosts on the Internet already prefer AES-256, so we’re practically there already—at least for the record processing!
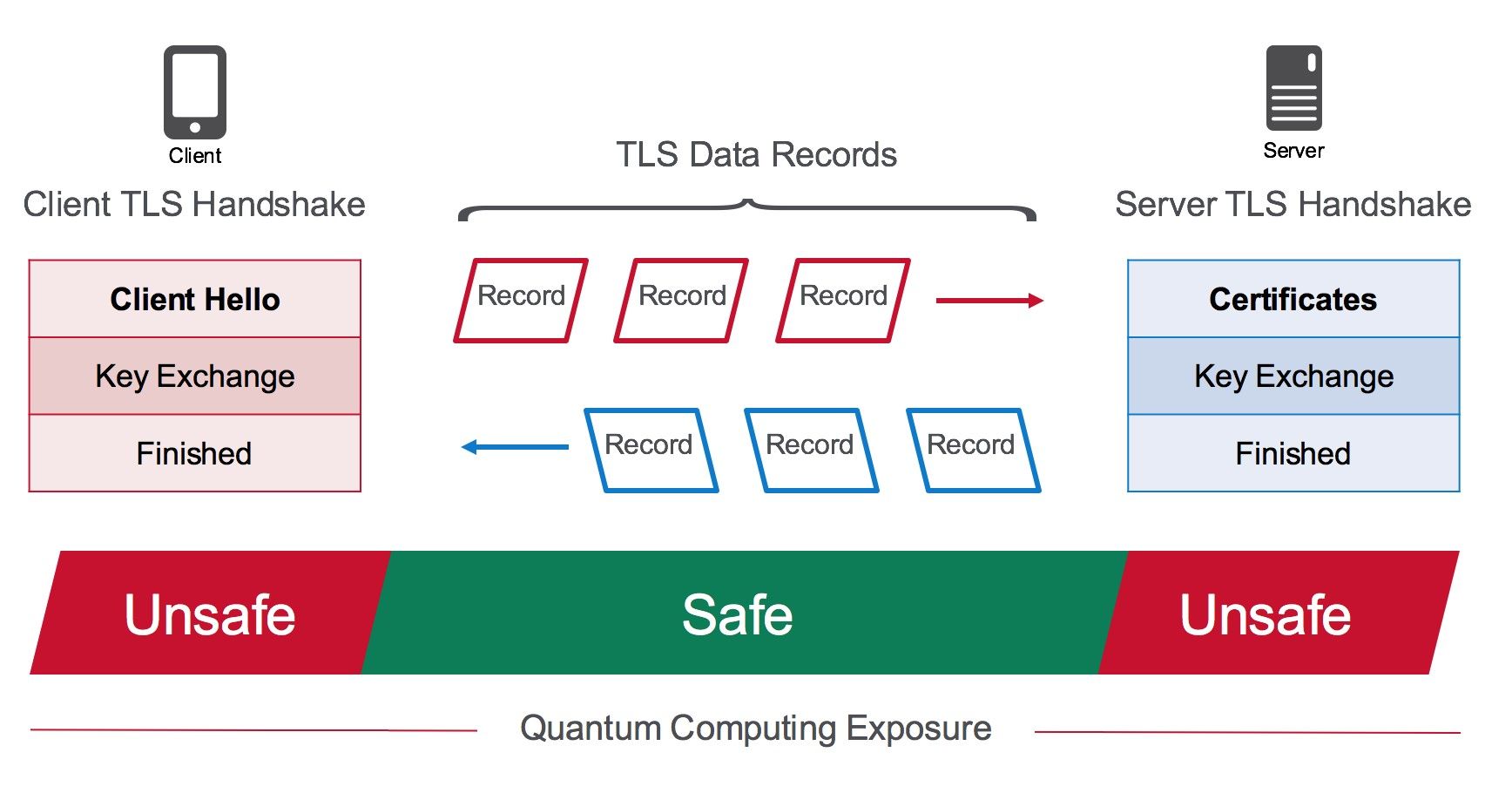
Figure 1. Quantum computing exposure, TLS 1.2 Protocol
Figure 1. Quantum computing exposure, TLS 1.2 Protocol
In 2015, several cryptographers provided initial recommendations in published white papers such as The Security and Performance of the Galois/Counter Mode (GCM) of Operation12 by David A. McGrew and John Viega, and The Poly1305-AES Message-Authentication Code13 by Daniel J. Bernstein. In Bernstein’s paper, he recognized that existing symmetric algorithms are quantum computing-resistant, but still recommends these options over the existing ones:
- AES-GCM using a 96-bit nonce and a 128-bit authenticator
- Poly1305
That leaves just the asymmetric encryption functions that need to be replaced: RSA, DSA, DH and their ECC variants, ECDSA and ECDH. Those are only used during the initial handshake phase of the TLS protocol, which for many clients is only done once per site, once per day, because of session reuse. That’s pretty good news when you think about it!
So, we don’t have to replace all of TLS, just shoe-horn in a new asymmetric handshake cipher. But which one will we use?
NIST Timeline for Choosing Post-Quantum Algorithms
The National Institute of Standards and Technology (NIST) has issued a timeline by which they would like to see a post-quantum algorithm ready to replace the existing asymmetric algorithms. At the time of this writing (summer of 2017), we’re currently in the submissions phase.
| TIMELINE | ACTION |
| December 20, 2016 | Formal call for proposals |
| November 30, 2017 | Deadline for submissions |
| November 30, 2017 | Workshop: Submitters’ presentations |
| 3-5 years | Analysis phase: NIST will report findings (1-2 workshops during this phase) |
| 2 years later | Draft standards ready |
In 2009 two NIST researchers, Ray A. Perlner and David A. Cooper, published a white paper examining the (then) likely post-quantum algorithm candidates. They included the chart below showing some of the algorithms’ comparative metrics against non-post-quantum algorithms (RSA, DSA, DH, ECC).
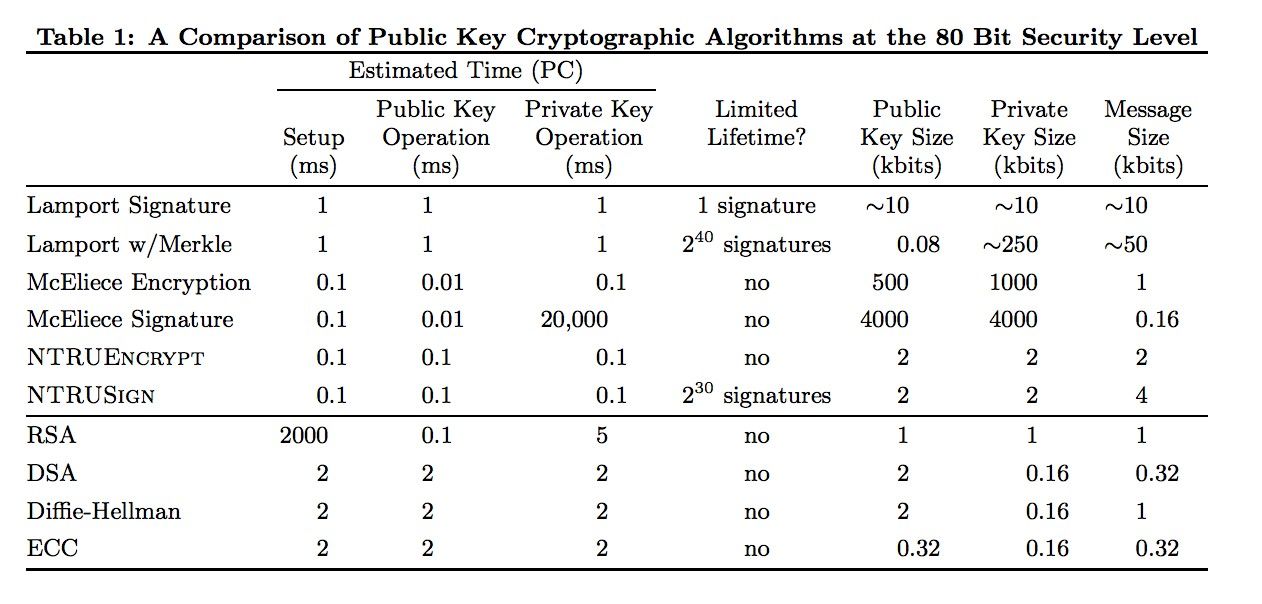
Since that paper was published, new algorithms have found currency in the community. However, the process of choosing one is a little like auditioning actors for the lead role in Hamlet. You quickly find that none are perfect and, in fact, some suffer from facial warts!
Current Candidates for Post-Quantum Asymmetric Encryption Algorithms
Several candidates are already being discussed, all of which have chosen key sizes that achieve the 128-bit level of security necessary to be quantum-safe. (Because the maths involved in each are complicated enough to boggle the mind, we won’t attempt to describe them here but provide instead the relevant Wikipedia links and wish you the best.)
NTRUEncrypt.14 One of the first post-quantum algorithms to gain notice was the NTRU (cutely pronounced “en-true”) which is based on lattice mathematics. Among its benefits are a supposedly low memory footprint and decent performance. A drawback is that a patent is involved, and history shows that open source projects tend to avoid patented algorithms.
McEliece with Goppa codes.15 One novel algorithm currently favored by some in the community is the McEliece encryption system. McEliece is the first algorithm to use randomization in the encryption process rather than in the key generation process, where most systems use it. One of its benefits is that it is faster than RSA, but its primary drawback is its huge keys. A typical RSA key is 2048 bits; a McEliece key is 512 kilobits! That’s 256 times as large!
Ring Learning with Errors. Another promising post-quantum key exchange method is Ring Learning with Errors (RLWE).16 It solves problems in field/set theory, and can also be used for homomorphic encryption,17 which is another darling at the crypto community ball. RLWE uses keys of 7,000 bits which, unlike McEliece keys, are in the same order of magnitude as today’s RSA keys.
Google actually publicly experimented with RLWE by combining a popular elliptic curve algorithm (Curve 25519) with a variant of RLWE called “New Hope.” A small fraction of Chrome browsers and Google servers (must be nice to control both sides of a TLS conversation) negotiated their key exchanges using this combined algorithm, which they dubbed CECPQ1.18 Google did not find any impediments to CECPQ1 other than an additional 1 ms delay, likely due to the larger key sizes. However, it has since ended its experiment with New Hope and is waiting for the IETF TLS committee to name a post-quantum winner.
Which is the Likely Winner?
The likely winner is an algorithm with a spectacularly bloated name: Supersingular Isogeny Diffie-Hellman (SIDH) key exchange.
SIDH has fewer warts than the other “actors” being auditioned. It:
- Uses the smallest key sizes of the candidates (3072-bit public keys)
- Can support forward secrecy
- Is free of patents19
SIDH is not perfect, though: some researchers have already been poking holes at it and have come up with some pretty disturbing attacks. The attacks can be mitigated against, but they add a whole new rash of warts.20
Related and Relevant IETF Projects
The IETF TLS working group has already started design work to fit a post-quantum algorithm into TLS. At the 93rd IETF in 2015, William Whyte proposed a hybrid handshake. Like Google’s CECPQ1, Whyte’s proposal uses a classical key exchange for half of the key, and a post-quantum key exchange for the other half. The two halves are then combined into a key derivation function to get the final master key, from which the rest of the session key data is derived.21
Conclusion
If it seems unlikely that any of these warty algorithms will make a good Hamlet, well, that’s okay. Many people in the crypto community are skeptical that a large-scale quantum computer is even possible. The largest number that’s been factored yet by the embryonic quantum computers is only 56,153.22 And that one was found accidentally; the researchers were only trying to factor the number 21. Twenty-one! That’s a far cry from factoring a typical RSA key.
Largest prime (accidentally) factored by quantum computers:
56,153
Representation of a sample 2048-bit RSA prime number:
57,553,458,486,056,431,746,847,208,022,543,120,686,362,765,031,041,714,
706,428,471,160,745,235,411,376,732,672,614,710,256,143,712,875,812,775,
531,754,663,720,746,448,566,758,301,438,002,242,338,424,048,764,872,084,
322,538,104,276,565,005,305,068,287,261,643,106,164,817,447,336,476,857,
633,361,313,702,487,483,684,380,181,504,352,488,756,401,348,372,666,675,
170,251,071,165,745,054,740,314,876,413,585,322,633,744,563,452,103,886,
563,380,208,134,638,771,150,750,348,252,338,443,643,674,024,137,867,731,
002,408,242,866,628,372,342,027,620,557,363,331,318,028,008,145,183,701,
081,845,364,150,033,761,083,575,482,476,712,010,033,513,666,101,161,535,
836,220,061,577,885,841,174,131,502,207,784,487,008,265,433,306,023,331,
401,716,233,713,633,513,551,554,050,487,048,463,525,706,858,664,265,067,
836,315,562,453,368,638,716,031
So, quantum computing still has a way to go. But if it really does become a thing, we’ll be (sort of) ready for post-quantum in pretty short order, at least from a protocol point of view. Adoption will take forever though, as usual.
Get the PDF version of this report: click “Download” below.